数理モデルとは
新型コロナウイルス(SARS-CoV-2)流行で、不安な方や、今後どうなるのだろうと気になる方が多いと感じます。感染症分野は、何らかの伝播によって疾病発生が引き起こされるために、数理モデルが有効だと思います。学内でも数理モデルを勉強したいという声を聞きますし、実際にモデルを作られてみると、social distancingの意義も伝わるかと思い、R shinyを利用して、SEIRモデルを実装したwebを作成しました。なお、作成者の横田は疫学の統計的理論を専門のひとつとしていますが、感染症分野や数理モデルについては勉強不足な部分が多いと思います。誤り等ありましたら、どうかご指摘ください。
SEIRモデルは、
- 免疫をもたない者 Susceptible
- 感染し、潜伏期間中の者 Exposed
- 発症者 Infectious
- 回復者(免疫獲得者) Recovered
という順番に人が遷移していく過程を常微分方程式でモデル化したものです。日本語による詳しい説明は、
- 西浦先生、稲葉先生が統計数理という雑誌に過去にレビューした論文(https://www.ism.ac.jp/editsec/toukei/pdf/54-2-461.pdf)
- 東大のヒトゲノム多様性研究室(http://www.bs.s.u-tokyo.ac.jp/~humgendiv/)
- wikipedia(https://ja.wikipedia.org/wiki/SEIR%E3%83%A2%E3%83%87%E3%83%AB)
などをご参照ください。最初にS,E,I,Rの4つの状態に存在する人数を指定し、遷移の速さを定める、
- R0, 基本再生産数(自然状態で1人の感染者が平均的に何人に感染させるか)
- average incubation period, 平均潜伏期間(Eになった者が次のIに遷移するまでの平均的な期間)
- average infectious period, 平均発症期間(Iになった者が他者へ感染を引き起こす期間)
を定めることで、将来予測を行える仕組みです。ここで、潜伏期間中は他者に感染させることなく、発症期間の最中だけ他者に感染させうるという定義としています。ちなみに、上記3つが導けるなら別のパラメータでも可能です。また、集団において死亡者と出生者がいることによって、人が入れ替わることは無視しています。
SARS-CoV-2に関して、Lauer先生らの論文(https://www.ncbi.nlm.nih.gov/pubmed/32150748)によると、incubation period(感染から症状発現までの期間として定義)は中央値で5.1日です。Eの人がIに遷移する期間の分布は指数分布に従うと考えることは自然ですから、incubation periodの中央値が5.1日ならば、平均値は7.35日となります。ヨーロッパ疾病予防管理センターのQ&A(https://www.ecdc.europa.eu/en/covid-19/questions-answers)ではinfectious periodは症状が出る人ならば、症状発現の1,2日前からスタートし、7~12日かかると説明されています。ということで、SEIRモデルを作るにあたって、平均潜伏期間は6日程度、平均発症期間は10日程度をwebツールでのデフォルト値と定めました。もちろん、症状がみられたら自主的に隔離する方が多いでしょうから、平均発症期間は10日よりもっと短い設定でいいかもしれません。
社会的隔離(Social distancing)の影響
感染症を放っておいた場合に一人からR0人だけ感染者を生むことになるわけですが、対策をとることで実際に感染者の発生を抑えることができます。例えば、はしかを引き起こす麻疹ウイルスのR0は10以上とされる、とてつもない感染力を示しますが、集団ワクチン接種により免疫をもたない者(S)を強制的に免疫獲得者(R)に変えてしまうことで、SからEへの遷移を減らすのです。SARS-CoV-2について、飛沫感染が感染経路と概ね分かってきたため、マスク着用や他者との距離を2m以上とる社会的隔離を現在可能な対策として行っています。
今は単純に、ある時点における1人の感染者が平均的に何人に感染させるかを表す実効再生産数Rtは、基本再生産数に接触頻度を削減(社会的隔離)できなかった割合を乗じたものとして考えることにします。例えば、R0は2.5だが、8割接触を削減できたら、2.5×(1-0.8)=0.5がRtとなります。
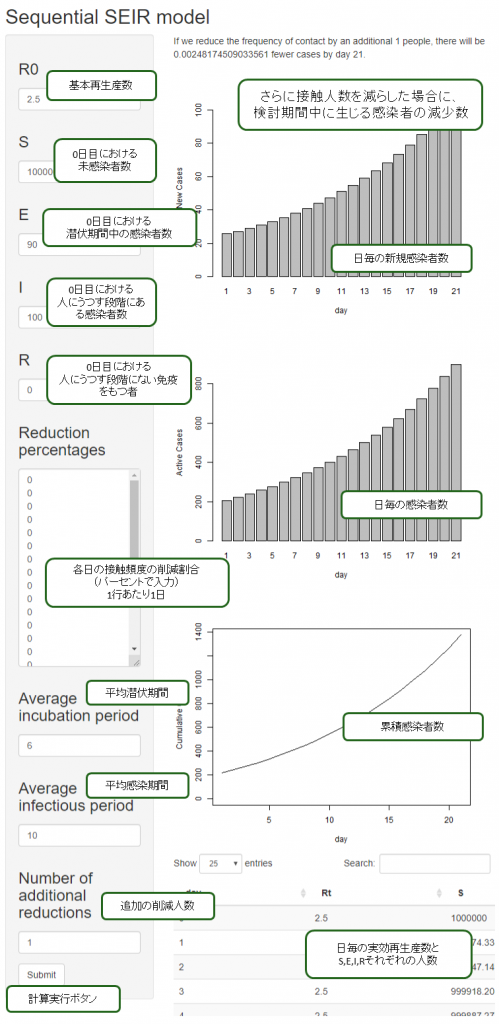
緊急事態宣言が発令されると、接触頻度は、数日かけて削減される経過をたどっています。何の指標を用いるかはさておき、webツールでは削減割合を入力することで、新規感染者数、入院中の数を図示します。1行が1日を表します。
さらにある人数の接触頻度を減らした場合に、検討する期間中に生じる感染者を何人減らせるかが計算されます。Sの初期値に対するNumber of additional reductionsの割合を、削減割合に加えた場合の結果を示します。負の値を入力すると、逆に接触頻度を増やしてしまった場合の結果を示します。
ちなみに、googleが人の移動量データを全世界、日本なら都道府県別に時系列で公開してくれています(https://www.google.com/covid19/mobility/)。
使い方
使ってみる(https://biostat-hokudai.shinyapps.io/seir/)
shinyを用いたRプログラムはこちら
R codes of SEIR model補足コメント(2020/5/6追記)
いろいろコメントを頂いていておりますので、いくつか説明を補足します。
本ツールで実効再生産数を求めることはできません
感染症数理モデルで将来予測をするためのツールであって、現在報告されている検査陽性者数等のデータを読み込ませて解析する、ということはできません。あくまで、何かしらの方法で得たパラメータ値から、将来の人口がどうなるのかを表すツールです。
接触頻度の削減割合の部分
本ツールにおいては、基本再生産数×(100% - 接触頻度の削減割合[%])/100%したものが実効再生産数に相当します。削減割合を1行増やすごとに1日分さらに予測することができます。一見ややこしい入力方法ですが、その分、様々なシナリオを作って比べることができるので、このような仕様にしました(sequentialと言っている部分です)。
じゃあ実効再生産数ってどうやって求めるのよ?
実効再生産数(effective reproduction number;効果的再生産数とも)は1人の感染者が平均何人に感染させるかを、(カレンダー時間だけでなく、感染の世代のような他の定義によるものでもよい)時点に応じて求めるものです。時点ごとに異なる値をとりうるので、実効再生産関数と呼んでもいいと思います。
非常に簡単な状況として、人が感染したら、必ず翌日の1日間だけ誰かに移す、かつ、感染者は瞬時に全員特定できるとします。すると、実効再生産数は前日の感染者を分母に、今日の感染者を分子においた比として点推定値は求められます。生成されるデータの不確実性(精度)を表す必要があるので、推定した信頼区間を併せて示します。
ただ、実際には、感染者がいつ、何日間にわたってうつすのか、また人によってうつしうる期間も異なるはずです。陽性と判断されるまでの期間や陽性と判断されないケースも考慮する必要もあるでしょう。他にもデータの生成過程から考慮しなければならないことはたくさんあると思います。完全に正確な値を1点で求めることは不可能ですから、ある程度、感染過程を考慮して実効再生産数に求めるにとどまってしまいます。例えば、感染してから他の人にうつすまでの平均日数が6日とするか7日とするかでも、その日数のばらつき(標準偏差)がいくつであるかに応じて、求まる実効再生産数は変わります。このように計算するにあたっての仮定を変えて解析する「感度解析(sensitivity analysis)」は観察研究で常に求められる内容です(STROBE statement; https://www.strobe-statement.org/)。実際に計算してみたい!ということでしたら、いくつかの計算方法であれば、以下に示すツールで可能です(申し訳ございませんが、使い方は論文等をご参照の上、各自でお願いします)。
- Cori先生らのExcelツール(京大・山中先生のwebでも使われていた)
https://academic.oup.com/aje/article/178/9/1505/89262 - Thompson先生らのwebツール
https://shiny.dide.imperial.ac.uk/epiestim/
ここは西浦先生の研究室ではありませんし、専門家会議とも何ら関係ありません
大学外の方からすると分かりづらい面があると思いますが、大学の各教室は個人事業主や中小企業に例えられると思います。で、西浦先生は「旧衛生学教室」、ここは「医学統計学教室」です。公衆衛生学コースという、公衆衛生を広く学び、研究する大学院を共に運営させて頂いていますが、本webツールに関しては、疫学の教科書にあるようなものを手軽に使えるようにしたにすぎません。
北大では、公衆衛生学教室の先生方が、保健所・自治体向けに感染者の状況を集計するツールを作られたり、呼吸器外科の先生が算数コロナ、とSIRモデルをより簡単な数値例で親しんでもらう企画をされたり、何より学生有志がNo More Coronaプロジェクトをしたりと色々な活動をされているようです。

勉強になりました。
素人考えですが、以下の係数が有ると良いと思いました。
地域性係数 1日1h出掛けた場合のウィルス接触率
発症係数 ウィルス接触量と抗体量から発症可能係数
医療崩壊係数 感染者受入れ可能数と感染者発症数による相関係数
無駄なコメント、申し訳ありません。
数理モデルの解説と公開ありがとうございます。すごく勉強になります。
お願いがあるのですが、隔離をモデルに組み込んでいただけないでしょうか。ソーシャルディスタンシング以外に、Exposed と Infectious を隔離によって減少させることで、感染を減少させることができますが、それを数理モデルで計算できるようにして欲しいです。
西浦先生の活動には非常に感謝しています。問題点は、現状では、ソーシャルディスタンシングしか考慮できないことです。現実に8割削減は非常に厳しいです。一方で、隔離にも難しい問題がありますが、政治と行政が頑張ればできるないことはないことだ思います。ソーシャルディスタンシングという国民へのお願いだけでなくて、隔離率を導入することで政治と行政の目標ができると思います。特に、家庭内感染を減少させることが課題だと思います。
参考までに、中国の研究者が隔離を考慮して感染者数を予測した論文です。
https://www.medrxiv.org/content/10.1101/2020.02.21.20026070v2.full.pdf
隔離のパターンを1パラメータに落とし込むことは困難と考えます。それは陽性者として特定されるまでの過程(クラスターの濃厚接触者として、もしくは症状を訴えたことによる検査)が経時的に変化することと、どのタイミングで隔離を行うかに依存するからです。
このwebツールは、比較的単純なモデルであるSEIRモデルにまずは慣れ親しんでいただくことを目的とし、対策班等から示される結果を自身で解釈しやすくなってもらうために開発しました。よりモデルを複雑化するにあたり、プログラムコードは公開していますので、適宜改変してご利用いただいて構いません。
命の為にありがとうございます。
「使ってみる」の使い方について質問です。
Reduction percentages、Number of additional reductionsの入力例を教えてください。
例えば60%削減だとどうなりますでしょうか。
Reduction percentagesに60と入力してください。
1行あたり1日を指します。
Number of additional reductionsは上記の削減割合後の世界において、さらにもうX人が全く他人と接触をしなくなった場合に何名の感染陽性者を減らせるかを別で計算するためのものです。
ご教示ありがとうございます。
Number of additional reductionsはいくつを入れても計算結果が変わらないように見えますが、どこが変わりますでしょうか。
また、Number of additional reductionsを用いて検査による隔離の効果として、乱暴ですが(検査数×陽性率)/2で入力すると検査隔離の影響がいめーじできませんでしょうか。
PCR検査数の増加の影響が知りたいです。
実効再生産性今後も重要な指標となります。COVID-19のウイルス排出の論文が出ています。山中教授のHPに乗っていますので、確認下さい。そこでは、潜伏期間、ウイルスが発症前2日前から増えて、発症後7日の間で減少すること。シリアルインターバル(発症から次の人が発症するまでの期間)を5.8日としています。初期の中国型ウイルスかもしれませんが、参考にして下さい。また、山中教授のHPに、アメリカのエクセルソフトでの有効再生産数算出の紹介もあります。合わせて、見て下さい。最後に、個人的に気にしているのが、無症状感染者の扱いです。例外対応するのは、発症者と同等以上居るのので、難しいと思います。是非、検討して頂き、ご教授下さい。https://www.nature.com/articles/s41591-020-0869-5 https://academic.oup.com/aje/article/178/9/1505/89262
参考になるページのご作成、公開を有難うございます。
モデル自体はオーソドックスな微分方程式のようで、おそらく専門家会議のモデルもそう違いはないようです。
一方、いくつかのパラメータのうち、潜伏期間等は得られやすいと思われますが、問題はR0, 基本再生産数かと思います。
これは、当初の専門家会議の説明では、ドイツの数値2.5からとったという説明があったと思います。
しかし、最近の専門家会議での資料では、0.5、0.7など、都度計算されているようです。
この数値は、我が国では、各クラスターを対象としたPCR検査の結果から得ていると考えてよいのでしょうか。
先ほど質問させて頂いた者です。先ほどの質問が舌足らずでしたので、補足をさせてください。
最近の資料の0.5や0.7は、実行再生産数のほうで、今でもR0←2.5でそこから0.5や0.7の実行再生産数を求めたものということでしょうか?
あるいは、当初はR0←2.5だったが、その後蓄積された検査結果のデータや、クラスター関連の検査結果による実際の再生産数も参照するなどして、ある時点から別途のR0の推定値が使われていて、それに基づいた実行再生産数でしょうか。それとも、0.5や0.7自体が、都度のR0の推定値でしょうか。
都度のR0というのはありません。
R0は感染症そのものが1人から平均何人にうつす能力があるかを表現したものです。
実効再生産数は、十分に感染が広まったり、人々が対策をとったりすることでその時点における当該感染症が1人あたり平均何人にうつるかを表現したものです。
https://ja.wikipedia.org/wiki/%E5%9F%BA%E6%9C%AC%E5%86%8D%E7%94%9F%E7%94%A3%E6%95%B0
ご回答有難うございます。
Wikipediaや入門書(Vynnycky,2010,An Introduction to Infectious Disease Modelling)も読んでみましたが、
ご指摘のWikipediaにも、
「基本再生産数 R0 は、環境因子や感染集団の行動による影響も受けるため、病原体に対する生物学的な定数ではない。」
というわけで、病原体に固有の、万国共通のR0があるわけではなく、
「基本再生産数 R0 の値は通常、数理モデルから推定される」「推定値は使用されたモデルや他のパラメータの値に依存する」
とのこと。また、
「文献における値は特定の文脈においてのみ意味があり、古い値を使用したり、異なるモデルに基づく値を比較したりするべきではない」
ともあり、当初日本のデータがないなかでは先行研究のR0←2.5を使ったとしても、その後は、
日本あるいは地域のデータの蓄積に応じて、あるいは気象条件など時期に応じて、基本再生産数R0は推定ないしカリブレーションして更新されていくべきものではないのでしょうか。
前のコメントによって誤解を招いてしまったら申し訳ございません。
実効再生産数とR0の違いについて述べていました。
頂いたコメントの通りで、R0は感染させる強さの初期値なだけなので、考える起算日や状況に応じて新たに推定した値でモデルを作り直すような場合に、異なるR0を用いるべきだと思います。
>ここで、潜伏期間中は他者に感染させることなく、発症期間の最中だけ他者に感染させうるという定義
ご存知かと思いますが、
COVID-19に関しては、無症状、つまり発症の2日程前から他者への感染があり得るとの可能性が指摘されていますね。
潜伏期間中は他者への感染はないとする定義の変更は見直さなくてよいのでしょうか?
>infectious periodは症状が出る人ならば、症状発現の1,2日前からスタートし、7~12日かかると説明されています。ということで、SEIRモデルを作るにあたって、平均潜伏期間は6日程度、平均発症期間は10日程度をwebツールでのデフォルト値と定めました。
Eのstateにいる間は人にうつさない、Iのstateにいる期間は人にうつす、としてご利用ください。
数式の公開、ありがとうございます。
感染者数というのは、PCR検査で診断された日と、症状が出た日のどちらから入力しているのでしょうか。
患者さんから聞き取った感染日や、感染経路不明者の推定感染日というのはパラメーターに影響するのでしょうか。
他の先生の質問にもありましたが、無症状陽性者のパラメーターはどのように入力されるのでしょうか。
院内感染の人数も少なくないようですがのようなケースはどのように入力されるのでしょうか。
あまりに基本的なことで、恐縮です。西浦先生のR Shiny コードをダウンロードして、RStudio上で実施実行しましたが、次のエラーが出て実行できません。
Stringr パッケージもインストールしました。 shiny, deSolveは使用経験があります。
/**************
Listening on http://127.0.0.1:7685
警告: パッケージ ‘stringr’ はバージョン 3.4.4 の R の下で造られました
警告: Error in : package or namespace load failed for ‘stringr’ in library.dynam(lib, package, package.lib):
DLL ‘stringi’ が見つかりません: このアーキテクチャ用にインストールされていないのでは?
****************/
stringi パッケージのインストールに成功しました。お騒がせしました。コメントを削除していただいても結構です。
SEIRモデルを修正して、無症状、軽症、中重症者別の検査隔離政策及び社会的距離政策を取った場合の必要病床、死亡者数、抗体獲得率を求める簡易エクセルシート(パラメタやモデルも単純な素人モデルですが)を作ってみたのですが、やはり当たり前の結果となりました。
1)検査率が低い、特に無症状や軽症者の検査隔離ができないと、大幅にsocial distancing政策で行動変容を求めない限り(非線形の微分方程式なので、優位な効果を得るにはある閾値が存在する?西浦先生がおっしゃている50-60%ではダメで80%が必要なこともそういうことなのでしょうか)、また周期的にそれを繰り返さないと、死者数が急激に悪化するし、その結果、医療崩壊となる。
2)もし無症状や軽症者も含めた検査隔離ができれば、ほとんどsocial distancing政策による行動変容をしなくても、死者数の増加や医療崩壊を防げる。検査隔離の徹底が(重症者はもちろん少しでも無症状や軽症者の検査隔離ができれば)死者数の増加を防ぐのに一番という結果になる。但し、無症状者や軽症者の収容をどうするかというインフラ上の問題や、そもそもどうすれば検査率を無症状者を含めて向上させられるかが、一番の鍵ですので、この方策が取れない間は生活様式の変容がやはり不可欠なのでしょう。
ウィルスの変異も言われていますし、一度抗体を持っても一定期間後にSやEの状態にクローズドループで戻ってしまう可能性もあるとしたら、どうなるのでしょうか。横田先生や西浦先生を含めた数理科学者と薬学、医学及び医療の力を結集して明るい未来ができるだけ早くやってくることを願います。
ありがとうございます。
>SEIRモデルを修正して、無症状、軽症、中重症者別の検査隔離政策及び社会的距離政策を取った場合の必要病床、死亡者数、抗体獲得率を求める簡易エクセルシート
気になります!
クローズドループはあり得るストーリーで、これまでのヒトコロナウイルスのように一定期間経過後に再び感染する、とかインフルエンザでみられるような、症状が落ち着いた後ぶり返すようなこともありえそうですよね・・。
現状わかっていないことが多すぎて、これからいろいろな人たちが議論、協力して対峙する感染症になると思っています。
現実のデータから、パラメータをどのように推定したかが何も開示されておらず、garbage in garbage out の典型例だと思いました。
実効再生産数の定義が曖昧に報道されています。一感染者があらたに感染させる数とされていますが、実際には一日当たりに感染させる数であるとおもいます。明確に、ご説明されることがリスクコミュニケーション上重要でしょう。
私の理解では「一日当たり」ではなく、一人が次の世代を何人生産するかです。すみませんが、一日当たりという話を聞いたことがないです。
より厳密には、一日とは限らず、特定の時点でと小生は理解しています。マスコミで公表されている値は、1日間の積分値ではないでしょうか。
たとえば、論文 [ref.1](未査読のようですが)での定義は、
“The effective reproduction number R(t) is defined as the number of secondary cases that an individual, becoming infectious at time t, will produce over time.”
また、次の論文[ref. 2]も次のように定義しています。
“The effective reproduction number can also be specified at a particular time t, presented as R(t) or Rt, which can be used to trace changes in R as the number of susceptible members in a population is reduced (…). ”
ここで、公開されているコード中のR_t は、実際には、基本再生産数(R0)ですね。
server.Rで、次のように R_t を定義し、
‘R_t <- input$R_t '
また、ui.Rで、次のように、入力ペインのラベル R0 の変数を R_t としていますから。
'numericInput("R_t", label = h5("R0"), value = 2.5)'
さらに、Server.Rでの計算式で、
dS <- -R_t/meani … などとされていますからそういえます。
マスコミで、「実効再生産数 1 人を切る」ことについて解説していますが、実際には、一日当たりだと思うのですがいかがでしょう。
reference:
[1] A. Arenas et al., ‘Derivation of the effective reproduction number R for COVID-19 in relation to mobility restrictions and confinement’, medRxiv, p. 2020.04.06.20054320, Apr. 2020, doi: 10.1101/2020.04.06.20054320.
[2] P. L. Delamater, E. J. Street, T. F. Leslie, Y. T. Yang, and K. H. Jacobsen, ‘Complexity of the Basic Reproduction Number (R0) – Volume 25, Number 1—January 2019 – Emerging Infectious Diseases journal – CDC’, doi: 10.3201/eid2501.171901.
感染率と回復率、再感染数の関係の理解に混乱がありました。質問を撤回します。
実効再生産数が今、世界中でコロナの拡散状況の判断基準と考えられていますが、PCR検査での検査データの検査数、基本再生産数などにより、変動すると思います。相対値としての比較は出来るが、絶対値としての判断は厳しいと考えます。しかし、ドイツなどが規制の緩和の判断基準とされています。どのようにして、実効再生産数を求めれば良いのでしょうか。教授願います。
公開されているというプログラムを見ないまま。コメントをしています。勘違いであった場合はご容赦。
>実効再生産数が1日当たりの感染させる数ではないかとの指摘がありましたが、元々の一般的なSIRモデルをみると、1感染者が感染者である間(完治するか死亡するまで。ただし総人数の変化は無視)に新たに感染させる人数となっています。2.5人というのは典型的な人口密度と行動モデル(ドイツ?)での感染初期での数値(1人の感染者が感染させる人数)と理解しています。実際には時定数に対応する係数がかけられていて結果的には指摘のように単位時間数あたりの人数に変換されているはずと理解しています。
>6割減では新規感染者数の変化が水平となるのは2.5*(1-0.6)=1となる。8割減は2.5*(1-0.8)=0.5を目指したものかと想像していますが、どうなのでしょうか。
もし、たとえば品川駅のでの乗降者数の減少率が8割減になっているかを気にするのであれば、通常時の実効再生産数がいくつで、それをどのくらいに減少させることを目途にしているかという議論が必要かと思いますが、どうでしょうか?
>外出自粛状態では、自宅に籠ってる人はこの統計の中から外れていることになっていませんか。言い換えると総人口が大幅に変化していることになりませんか。
元々のSIRモデルでは、感染者数の増加は、感染者一人の感染可能者に感染させる確率と接触する感染可能者数の積と既感染者数に比例すると近似されてます。(回復はここでは考えない)結果的には新規感染者数は、接触する感染可能者数のみならず感染者数にも比例します。感染の多くが駅や観光地の密集で起きるとする場合、感染に関与する感染者、感染可能者の両方が、このモデル式に含まれていない(すなわち、外出自粛など)ことで大きく変動する場合(総人口が保存されていない)このモデルはこのまま使用できますか?、
コメントの内容にほぼ同意です。そもそも濃厚接触による伝播が強く考えられ、実際に病院や老健施設での大規模クラスターが発生していることから、1人が何人に感染するかの分布自体がPoisson分布のような類の分布からはoverdispersionしていますし、接触の削減割合なんて完全には定量化できないと思います。もちろん、単純なSEIRモデルでは隔離の影響、集団の流入、流出も考慮できないと思います。不顕性感染が少なからずいると指摘されるSARS-CoV-2感染では、Eに移行する定義を陽性確定なのか感染なのかで話は大きく変わると思います。個人のtwitterにおいて、「多分、西浦先生たちのグループはこうした古典的数理モデルをもはや使っていないと思います」と本ツール公開当初に感想を述べましたが、その根拠は上述の通りです。
とはいえ、疫学理論をやっている身としては、現実世界を抽象化・簡略化したものがモデルであり、間違っているから全く使えないとは考えずに、感度解析を行って多角的な検討をしたいと思うのです。その議論の土台となるべく、簡単な数理モデルに親しんでいただき、その特徴を感じてもらって、次の発展的な議論に進んでもらえたらなという思いで公開しています。
単純なSEIRモデルで状況を単純化して、傾向性を見る事も必要と思います。(相対比較)
しかし、国の緩和の判断基準とするのであれば、式で使用する値(基本再生産数、実際の感染者など)が
十分に実態に合っていることが必要と考えられます。その検証はされているのでしょうか。教授願います。
実効再生産数を調査感染曲線から求めるR Package が存在します。
https://wp.me/p264xJ-Nx
参考になる数理モデルの解説ページの公開を有難うございます。
この感染症とは長期間に渡って世界的に対峙することになりますが、実効再生産数を如何に低減する行動変容などの対策(施策)の効果を興味を持っております。
ここのコメントにもあるように、ウイルスの量が非常に高くなり伝染力が高い時期(発症初期)に感染者(罹患者)を判別し、早期に市中から隔離(自主隔離を含む)できるかがポイントと考えています。
行動変容などの対策(施策)は各国の国柄によってかなり異なりますが、日本における緊急事態宣言の解除後(6月以降)の状況を数理モデルで一定範囲で予測できないかとも考えています。
例えば、感染ピークの第一波を乗り越えて制限緩和し、第ニ波ともなりかないクラスターを発生している韓国、中国、シンガポールなどと対策(施策)の観点から日本と比較すると、いろいろな知見が得られるのではと・・・
・韓 国
ソウル市 イテウォンクラブ関連 クラスター
https://www.seoul.go.kr/coronaV/coronaStatus.do
・中 国
吉林省 舒蘭市
https://k.sina.cn/article_1655444627_62ac1493020017x3l.html?cre=wappage&mod=r&loc=3&r=9&rfunc=60&tj=none
http://www.jl.gov.cn/szfzt/jlzxd/yqtb/202005/t20200513_7215725.html
http://www.jl.gov.cn/szfzt/jlzxd/
・シンガポール
外国労働者の宿舎施設
※Google Chromeの翻訳機能で閲覧しています
上記の国々はITツール(濃厚接触通知アプリ)、来場者名簿、クレジットカードの利用歴、防犯カメラ、携帯基地局の位置情報まで活用して2~n次感染者を特定し、さらには発症前後から市中からの隔離まで行動履歴を公開して積極的な検査を受けるようにしています。
※韓国の場合、今回のクラスターは性的少数者(LGBT)コミュニティーに
関わる特殊事情があるにしても感染拡大の危機は高いかと。
たぶん日本ではプライバシー(個人情報保護)の観点から同様なことはできないかとは思っていますが、日本国民ならでは一歩踏み込んだ意識変革した行動変容ができればと思っています。
※日本版 濃厚接触通知アプリ等
https://www.nikkei.com/article/DGXMZO58934680R10C20A5000000/
https://www3.nhk.or.jp/kansai-news/20200512/2000029566.html
日本の緊急事態宣言の解除後(6月以降)は、一律的な「人との接触8割減」ではなく、「感染者との濃厚接触を8割減」を目指すことが喫緊の課題と思っています。
日本に比べて韓国では感染者の濃厚接触者の早期PCR検査の受検を強く推奨していますので、期間限定ですが感染者(陽性者)の行動履歴が情報公開されています。
次の報道にあるイテウォンキングクラブで感染した方が2~4次感染とクラスター化した行動履歴を追える仁川広域市のサイトがありましたので共有させていただきます
梨泰院クラブ訪問「仁川塾講師」関連の新型コロナ感染者、13人に
http://m.jp.ajunews.com/view/20200514101052113
なお、以下のとおり「確定患者が最後の接触者と接触した日から14 日経過して時点」で削除され、現在、閲覧可能なケースはNo.98~143となり、上記の塾講師はNo.102となります。
また、当方は韓国語はわかりませんので、ブラウザのGoogle chrome translatorを使って閲覧しています。
※参考 https://pc-karuma.net/chrome-translator-toolbar/
この公開情報をみていると、個体差はあるものの感染後に48時間ぐらいでウィルスが体内で増殖し、自覚のない無症状の段階の12時間ぐらいはウィルスを拡散し、更に12時間ぐらいすると自覚症状が発現するのが読み取れるケースが何件かわかります。家庭内感染もわかります。
この”魔の一日”(自覚のない無症状の段階の12時間ぐらいはウィルスを拡散)が緊急事態宣言の解除後に厄介な期間なるかと。
ただ、韓国当局の取り組みとしては”濃厚接触者の早期PCR検査の受検”を強く推奨しているケースとして、自覚症状が発現する前に受検して陽性者の市中からの早期隔離を成功している事例もありました。
********************
コロナウイルス感染症-19仁川広域市の現状
https://www.incheon.go.kr/corona19/IC010001
********************
公開範囲
感染症患者の移動経路、接触者の現況などの情報公開は、力学的な理由、法令上の制限、感染者のプライバシーなどの多角面を考慮して、感染症の予防に必要な情報に限って公開する
(個人情報)の個人を特定する情報を開示していない*国家人権委員会勧告(’20 .3.9)
(時間)コロナ19は、症状発生2日前から隔離日まで
(場所・移動手段)確定者の接触者が発生した場所と移動手段
※時間・空間的に感染を心配するほどの確定者との接触が起きた場所や移動手段を公開する
※その領域内のすべての接触者が把握された場合、公開しないことがある
中央防疫対策本部の「確定患者の移動経路などの情報公開案内(2020.4.12)」に基づき、「確定患者が最後の接触者と接触した日から14 日経過して時” 確定者の動線を非処理
*********************
“★ <= " 当方が付記した補足
——— No.102の患者の行動履歴から一部抜粋
102. #10847 ミチュホル区 (南1995年生まれ/ 2020.05.09 /イテウォン))
2020.05.02〜2020.05.03
イテウォンキングクラブ、パブ訪問 ★ <= ここで感染
2020.05.06
(17:00)龍現洞素材飲食店(知人の車利用)
(18:00)耳(徒歩)
(19:00〜23:00)立てる塾の講義(タクシー利用、マスク未着用)★ <= ここで2次感染拡大
★ <= 10人へ感染させる
103 2020.05.09 #10900 ミチュホル区 (南1986年生まれ" "梨泰院確定者(102)の接触者(知人)))"
109 2020.05.13 #10963 ミチュホル区 (南2005年生まれ" "仁川確定者(102)の接触者(同じ学園の学生)))"
110 2020.05.13 #10982 中区 (女2004年生まれ" "仁川確定者(102)の接触者(同じ学園の学生)))"
111 2020.05.13 #10981 中区 (女2004年生まれ" "仁川確定者(102)の接触者(同じ学園の学生)))"
112 2020.05.13 #10979 中区 (女2004年生まれ" "仁川確定者(102)の接触者(同じ学園の学生)))"
115 2020.05.13 #10967 ミチュホル区 (女2002年生まれ" "仁川確定者(102)の接触者(同じ学園の学生)))"
116 2020.05.13 #10966 ミチュホル区 (南1999年生まれ" "仁川確定者(102)の接触者(塾講師)))"
113 2020.05.13 #10969 延寿 (女2007年生まれ" "仁川確定者(102)の接触者(家庭教師)))"
★ <= 4人の3次感染へ
125 2020.05.17 #11068 南洞 (南1954年生まれ" "仁川確定者(102)の接触(タクシー運転手)))"
★ <= 3人の3次感染へ
119 2020.05.13 #10990 南洞 (南2002年生まれ" "仁川確定者(102)の接触者(同じ学園の学生)))"
★ <= 4人の3次感染、2人の4次感染へへ
2020.05.08
(18:22)ミチュホル区保健所選別診療所(徒歩)*無症状 ★ <= ウィルスを拡散???
★ <= イテウォンキングクラブ者のため受検
2020.05.09
(02:58)陽性判定→仁荷病院音圧病状の治療
——— No.119の患者から4人の3次感染 ※濃厚接触者
121 2020.05.13 #10996 南洞 (女1978年生まれ" 仁川確定者(119)の母))
122 2020.05.14 #10999 ミチュホル区 (南2002年生まれ" "仁川確定者(119)の接触(友達)))"
133 2020.05.19 #11098 ミチュホル区 (南1997年生まれ" "仁川確定者(119、122)の接触、コインカラオケ))"
128 2020.05.19 #11083 ミチュホル区 (南2003年生まれ" "仁川確定者(119、122)の接触(コインカラオケ)))"
★ <= 2人の4次感染へへ
——— No.128の患者から2人の4次感染 ※濃厚接触者
127 2020.05.19 #11084 ミチュホル区 (女1974年生まれ" 仁川確定者(128)の母))
132 2020.05.19 #11097 ミチュホル区 (南1971年生まれ" 仁川確定者(128)の父))
——— No.122の患者の行動履歴から一部抜粋
122. #10999 ミチュホル区 (南2002年生まれ/ 2020.05.14 /仁川確定者(119)の接触(友達)))
20.05.06
南洞区確定者(インチョン119番)と龍現洞ビジョンプラザたPC部屋(11階)、タワーコインカラオケ(2階)を訪問
20.05.08
(20:10)自宅出発(親車両利用、マスク未着用)
(20:30〜23:00)延寿内の勉強部屋の講義受講(マスク着用)
(23:20)自宅帰宅(先生車両利用、マスクの着用)
20.05.09
(17:10)自宅出発(親車両利用、マスク未着用)
(17:30〜19:30)延寿内の勉強部屋(マスク着用)
(19:30)延寿素材飲食店(歩行、マスク未着用)
20.05.10
自宅にモムム *発熱、咳などの症状発現 ★ <= 症状発現 5/9あたりからウイルス拡散???
20.05.14
(07:40)陽性判定→仁川医療院音圧病床隔離
お世話になります。
実効再生産数を計算する際にインプットする市中感染者数について教えてください。
PCR検査で毎日確認される陽性率は、感染ピーク時には症状が強い陽性確率の高い人の検査が多く実際の感染率より高くでて、
感染収束時にはかぜ症状の人も検査を受けるようになり実際の感染率に近づくと思います。
このことに関する検査陽性率→実際の感染者数の変換の方法論はありませんでしょうか。
私は全くの専門外ですが、興味本位でSIRモデルに感染確率Pi(t)と回復確率Pr(t)を時間の関数として組み入れたモデルを作りました。
さらに、隔離がある場合についても隔離率εと隔離確率Pq(t)を組み込み、FORTRANで計算して良好な結果を得ました。
このようなモデルは疫学の分野では既に知られているものでしょうか?
なお、論文の形にまとめましたので、ご連絡いただければお送りします。
以上、ご教示いただけたら幸甚です。
東京都のコロナのこれからの予想を、教えてください。よろしくお願いいたします。
返信されていたことに気づきませんでした。申し訳ありません。
計算では、現在の状況は実効再生産数1.35前後で、このまま放置すると10月末にピークを迎えます。
ピークでは感染者数が95万人となり、その後感染者数が減少に転じますが、新規感染者数がゼロ近くになって収束する頃には既感染者数は660万人程度になります。
ただ、最近一週間の新規感染者数の増加割合が大きいので、実際にはもう少し早まる可能性があります。
SEIRモデルについて、3つ質問させてください。
1) 未発症で感染源になる場合は、考慮していますか?
方程式上は、簡単に組み込むことが可能かと思いますが、その場合、Eの「日数別分布を仮定する」することになるかと思います。
言い換えれば、上述の average infectious period の定義は、COVID-19の状況に則していないのではないか、と思っています。
(対応されているのなら、ごめんなさい)
2) 回復者の者の再感染は考慮されていますか?
一般的なSEIRでは、Rは免疫を持っているため、再感染することが無いことが前提かと思います。
しかし、実際は再感染もしくは再燃が幾例か報告されています。
その状況に鑑みて、SEISの方が実態を表しやすいのではないか、とも思っています。
(再感染が Negligibleであれば、SEIRで良いのですが)
3) SEIRは、S→Eを確率(衝突断面積)で表しています。ここが確率ということは、ネットワーク理論で言えばランダムネットワークです。
クラスター対策を用いるということスケールフリーネットワークが有効な場合だと考えると、根本的に矛盾しているように感じます。
SEIRモデルの適用限界ではないかとおもうのですが、如何お考えになりますか?
一つ分からないところがあるので教えて下さい。
Average infectious periodの部分に数字を入れてみたのですが、この期間が長くなればなるほど累計感染者数が減少していきます。
他人に感染させる期間が長いほど感染者は増えるのではないでしょうか。
自分の勘違い、理解不足であったら申し訳ありません。
こちら私も疑問に思っておりまして、ご教示いただけますと大変助かります。
>一つ分からないところがあるので教えて下さい。
Average infectious periodの部分に数字を入れてみたのですが、この期間が長くなればなるほど累計感染者数が減少していきます。
他人に感染させる期間が長いほど感染者は増えるのではないでしょうか。
自分の勘違い、理解不足であったら申し訳ありません。
教えてください。最近、SEIRモデルの意義づけが分からなくなってきました。
理由は、発症前に感染させる可能性が相当高いという新型コロナの特徴です。
感染者の発症前と発症後の感染はほぼ半々という報告もあると思います。そうすると潜在期間とは何でしょうか?
外見的には症状はなくとも感染させる患者を変数Eに入れてよいのでしょうか?
また微分方程式の1番目と2番目に入っているβSIの項は感染者Iからウイルスをもらって未感染者から発症前感染者に移る人数を示していますが、このほかに発症前感染者からウイルスをもらって新たに発症前感染者に移る人数を表す項(例えば、β’SE)も加える必要があるのではないのでしょうか?
たまたま、このサイトにぶつかりました。政府分科会は、COVID-19の第5波が急減したことの説明が未だにできないようです。SIR系の数理モデルを扱う研究者にとっては、当然のことが起きたと思っていますが、残念ながら、政府分科会には数理モデルの専門家はいないようです。多くのSIR系のモデルは、連続する感染波の解析まで踏み込んでいないようです。SIR系の数理モデルは、高々1次の微分方程式ですから係数が一定であれば振動することはありません。結果が振動する(次々と感染波が起きる)ためには、係数が周期的に変化するか(パレメーター励振)、保存則を仮定している人口が増加する必要があります。この仮定に基づいて数理モデルをデータ適合により計算すれば、感染が始まって波が成長を始めると精度高い予測計算ができます。東京都第5波の場合は、8月5日の計算でピークアウトも含め、1か月先まで正確な新規感染者の予測計算が出来ていました。将来の感染波(今は第6波)については、いくつかの仮定が必要なので、仮定の下での計算になりますが、見通しの良いシミュレーションんができます。PDFを送る方法をご連絡いただければ、もう少し詳しい説明を送ります。日々公表されるデータを予測計算できるので、数理モデルに関心がある学生さんの興味も増大すると思います。
大変有用なツールをありがとうございます。中学の修論に引用したいと思っております。
Eにどの数を入れたらよいのかわかりません。「潜伏期間中は他者に感染させることがないが、感染し、潜伏期間中の者」として、何が該当しますか?
感染者と接触があった人数で、発症二日前の人数ですか?